Sizes of Models in Salome

Table of Contents

• Maximal Size of the Model
• Minimal Size of the Model
• Full Range of Sizes

In Salome and Open CASCADE Technology (OCCT), which is a modeling core of Salome GEOM module, any model has its location in the 3D-space and size.

This document defines the range of values (tolerances, locations and sizes) that should be taken into account for any 3D model design.

It is not obligatory to create models within this range, however, algorithms can fail or return unexpected results if the recommendations are not followed.

Maximal Size of the Model

The Maximal Size of the model corresponds to the maximal diameter of enclosed sphere built for the model. In OCCT any model has a location defined relatively to the absolute origin. Thus the maximal diameter should be built taking into account the model itself and its location.

In OCCT there are two tolerances: Tolerance Confusion (TolC) and Tolerance Angular (TolA) (see OCCT Precision package for more details). These values are used for geometric comparisons. However, they are not used inside low-level algorithms (e.g. intersection), where more precise values are used instead. The value TolC guarantees that the error associated with the computations for a given geometric entity is not greater than TolC.

• TolC - precision value used to check the coincidence of two points [by default 1.e-7];
• TolA - precision value used to check the equality of two angles [by default 1.e-12].

For more information on tolerance definition please see Chapter 4 of this document. To see limitations that are due to modeling errors or inaccuracies of tolerance usage please refer to Chapter 9.2.2 of the same document.

To provide robust geometric modeling the computations should be consistent, i.e. the one tolerance value should be used for all computations. Thus, the TolC and TolA values should be consistent:

Smax = TolC / TolA             (1)

TolC, TolA and Maximal Size Consistency

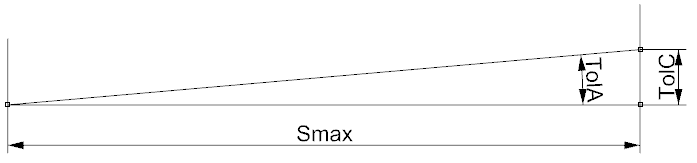
In accordance with (1) the Maximal Size for the Model is [by default]:

Smax = 1.e-7 / 1.e-12 = 1.e+5  (2)

Minimal Size of the Model

The Minimal Size of the Model is defined as the maximal diameter of enclosed sphere built for the smallest BRep entity of the Model.

All models in OCCT are represented using double precision floating point numbers. This representation contains approximately 14-16 significant digits.

From the experience, it is considered that the last four significant digits contain rounding-off errors occurring during the computation. So (taking into account the worst cases), there are ten reliable significant digits for double precision floating point numbers. Having the estimation it is possible to compute the value of the Minimal size of the model:

Smin=Smax / 1.e+10             (3)

In accordance with (2) for the default value it will be [by default]:

Smin=1.e-5.                    (4)

Full Range of Sizes

The values Smax (2), Smin (4) are theoretical. Taking into account the practical purposes of improving the reliability, the lower limit should be restricted by one order. Thus, the full Range of Sizes of the Models is:

[Smin, Smax] = [1.e-4, 1.e+5]  (5)