Mapped barycentric intersection type ('MappedBarycentric') can be selected in space dim 2 (resp. 3) when working with quadrangle only (resp. hexaedrons only).

It can only be used for P1P1 projection: for any point P within the quadrangle or the hexaedron, the set of reduced coordinates is computed (x, y, z all comprised between 0 and 1). Then the field value at P is computed using the usual form functions of finite element method ((1-x)*(1-y), x*(1-y), (1-x)*y and x*y in 2D for example).

The algorithm used to compute the reduced coordinates differs in dim 2 and dim 3.

Dimension 2

Let O, A, B, C the four points of the quadrangle, clockwise. Without loss of generality O is assumed to be the origin. A point P within the quadrangle is identified with vector OP and simply denoted P.

A suitable mapping is such that, if (x,y) is the couple of reduced coordinates (with x and y both in [0,1]) of a point P, then:

$\mathbf{P} = x\mathbf{C} + y\mathbf{A} + xy(\mathbf{B}- \mathbf{A}-\mathbf{C})$

This forms is the simplest one having a gradient which x component is constant in x, and similarly in y. Furthermore the reduced coordinates (0,0) (resp. (0,1), (1,0), and (1,1)) map to point O (resp. A, B, and C).

Calling 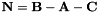$\mathbf{N} = \mathbf{B}-\mathbf{A}-\mathbf{C}$ and developping for the 2 compos:

$p_x = C_x x + A_x y + N_x xy$

$p_y = C_y x + A_y y + N_y xy$

Solving the first eq for x:

$x = \frac{p_x - y A_x }{C_x+yN_x}$

and injecting in second eq:

$(A_yN_x -N_yA_x)y^2 + (-p_yN_x -A_xC_y +A_yC_x+N_yp_x)y + (p_x C_y-p_yC_x)=0$

solved in:

$y = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2a}$

where a, b and c are the coeffs of the 2nd order eq.

This gives two possible couples of solution among which only one is in $[0,1]^2$ .

In case where 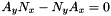$A_yN_x -N_yA_x = 0 $ we have a degenerated unique solution for $y$

$y = \frac{c}{b}$

Finally it is worth puting aside the case 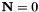$\mathbf{N} = 0$ (rectangle), which boils down to solving an ordinary 2-unknows system:

$x = \frac{p_x A_y - p_y A_x}{C_x A_y - C_y A_x}, y = \frac{C_x p_y-C_y p_x}{C_x A_y - C_y A_x}$

Dimension 3

In three dimensions, adopting the same approach as above would lead to a 4th order equation to solve. A simpler approach has been chosen: the distance to each pair of parallel faces in the hexaedron is computed. The ratios to the sum of the two distances is computed giving again a number between 0 and 1 for each of the 3 directions.