Odprtokodno CAD-jedro OpenCASCADE

(angl. Open code of CAD core OpenCASCADE)

Uvod

Za modeliranje posameznih 3D-elementov in prenos modelov med programi CAD z uporabo formatov STEP/IGES poljubne konstrukcije uporabljamo tudi odprtokodna CAD-jedra. Komercialni modelirniki CAD, ki jih ponujajo na trgu, so po eni strani bolj univerzalni, po drugi strani pa zaradi univerzalnosti pri specifičnih postopkih modeliranja nimajo ustreznega odzivnega časa ali pa so postopki modeliranja preveč zapleteni. Odprtokodno CAD-jedro je namenjeno specifičnim oblikam, ki so sicer kompleksne. Pri določenih postopkih modeliranja lahko posamezne korake usmerjamo in jih po potrebi standardiziramo za določene procese modeliranja. Modeliranje je namensko, zato je časovno bistveno krajše. To pa je že prednost pri modeliranju posebnih oblik. Med prvimi je CAD-jedro z imenom Open CASCADE v modelirniku EUCLID uporabljala Matra Datavision (od leta 1982 do leta 1990). Laboratorij LECAD na Univerzi v Ljubljani je bil tudi na tem področju med razvojnimi uporabniki tako zasnovanega programskega jezika. Open CASCADE je informacijsko tehnološko podjetje, ki opravlja storitve na področju znanstvenega in tehničnega računalništva, zlasti z integracijo orodij za simulacijo. S pomočjo CAD-jedra Open CASCADE je mogoče razviti posebne rešitve, ki poleg splošnega modeliranja vključujejo znanje vsakega posameznika. Družba Open CASCADE se opira na mednarodne skupine visoko usposobljenih kadrov na področjih 3D-modeliranja, izmenjave podatkov, numerične simulacije, vizualizacije in grafičnih uporabniških vmesnikov. Predstavljene možnosti na področju simulacij zagotavljajo, da Open CASCADE nastopa kot pomemben, morda celo glavni akter na področju simulacije. CAD-jedro se uporablja za izdelavo specialnih 3D-modelov in njihovo vizualizacijo. Podjetja in razvojne ustanove, ki razvijajo elemente najzahtevnejših procesov modeliranja, predvsem na področju simulacij, uporabljajo Open CASCADE zaradi odprte kode in kompleksnega obvladovanja geometrije v prostoru. Pri tem moramo poudariti enostavnost določenih transformacij, ki posredno omogočajo procesiranje v realnem času ob relativno majhnih računalniških kapacitetah. Knjižnice CAD-jedra, ki omogočajo 3D-modeliranje in vizualizacijo, uporabljamo s pomočjo programskih jezikov C++, Python, Java v različnih operacijskih sistemih (Windows, Linux, Solaris). Licenca tehnologije Open CASCADE je brezplačna in prosto dostopna za uporabo v gospodarsko razvojnih okoljih. Za učenje uporabe obstaja prosto dostopna pomoč za prikaz splošne uporabe in uporabe na geometrijskih 2D- in 3D-primerih. V nadaljevanju bomo uporabljali skrajšano ime za Open CASCADE, in sicer OC.

Zmogljivosti jedra OpenCASCADE

CAD-jedro OC je zgrajeno iz posameznih modulov, ki mu omogočajo obvladovanje različnih funkcij. Posamezna funkcija se smiselno uporablja za modeliranje poljubnih 3D-modelov. CAD-jedro OC je sestavljeno iz naslednjih modulov: osnovni razredi, modeliranje podatkov, algoritmi za modeliranje, mreža, vizualizacija, izmenjava podatkov (STEP/IGES), aplikacijska ogrodja, grafični uporabniški vmesnik in razvijalna orodja.

Modularna struktura CAD-jedra Open CASCADE

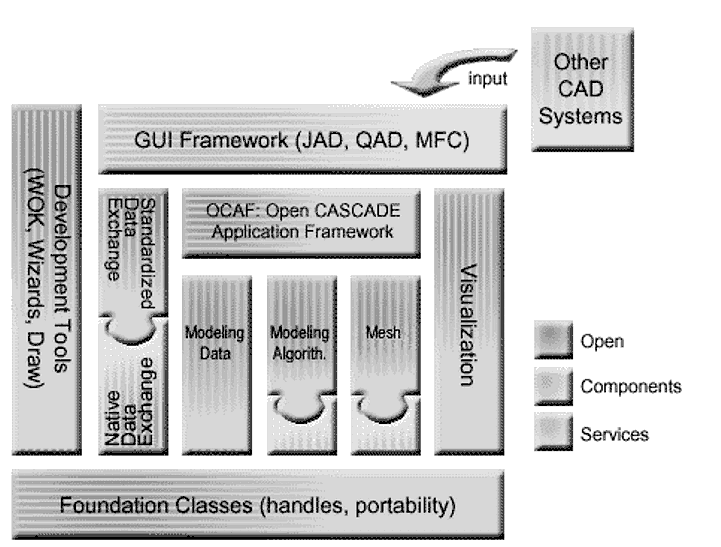
Slika 1. Modularna struktura tehnologije Open CASCADE

Other CAD systems: Ostali modelirniki CAD
Input : Vstop v OC
GUI Framework (JAD,QAD,MFC): Programski okvir GUI (JAD, QAD,MFC)
Developmnet Tools (WOK, Wizards, Draw): Razvojna orodja (WOK, Wizards, Draw)
Standardized Data Exchange: Standardizirana izmenjava podatkov
Native Data Exchange: Priprava podatkov iz okolja
Modeling Data: Modeliranje podatkov
Modeling Algorithm: Algoritmi za modeliranje
Mesh: Mreženje prostora za prikazovanje Foundation Classes (handles, portability):
Osnovne transformacije (glavna knjižnica, matematična orodja, manipuliranje s podatki)
Visualization: Predstavitev – vizualizacija
Open, Components, Services: Odprti dostop, komponente – osnovne, vzdrževanje

Na sliki 1 je prikazana struktura in modularna zgradba OC. Predstavljena je sestava in pozicija posameznega modula v OC. V nadaljevanju bomo predstavili značilnosti vseh pomembnih vsebin posameznih modulov.

Osnovne transformacije (ang. Fundation Classes)

Primitivni tipi, nizi in različni številski tipi Avtomatizirano upravljanje s spominom Obvladovanje izjemnih situacij Razredi za manipulacijo grupiranih dokumentov Matematična orodja: vektorji, matrike Osnovne storitve za shranjevanje podatkov v datoteke ASCII

Osnovna podpora za manipuliranje, transformacije in pripravo podatkov za vpis v bazo je razdeljena v tri knjižnice: glavna knjižnica (kernell classes), matematična orodja (math utilities) in manipulacija podatkov (basic data storage).

Glavna knjižnica (ang. Kernell classes)

Knjižnica je namenjena obvladovanju osnovnih podatkovnih tipov, kot so Boolean, Character, Integer ali Real, optimizaciji in upravljanju spomina.

Matematična orodja (ang. Math utilities)

Matematična knjižnica je namenjena obvladovanju matematičnih algoritmov, ki vsebujejo osnovne operacije z vektorji in matrikami, izračunavanju (solve) linearnih algebraičnih enačb, algoritmov za iskanje rešitev nelinearnih enačb, algoritmov za iskanje minimalnih vrednosti funkcij. Poleg algoritmov vsebuje podprograme za izdelavo geometrije točk, črt, krogov, ravnin (points, vectors, lines, circle and conics, planes and elementary surfaces).

Manipulacija s podatki (ang. Basic data storage)

Knjižnica za shranjevanje podatkov se uporablja za organizacijo in manipuliranje s podatki. Omogoča zapisovanje in branje podatkov v datotečne sisteme.

Modeliranje podatkov (ang. Modeling data)

Modul podpira podatkovne strukture za predstavitev dvo- in trodimenzionalnih geometrijskih in topoloških modelov. Omenjene strukture so vključene v naslednjih knjižnicah: 2D Geometry, 3D Geometry in Topology. Topologija je sklop pravil, ki definirajo geometrijske povezave med objekti v prostoru (točke, linije). 2D Geometry. Ta knjižnica zagotavlja dvodimenzionalne geometrijske strukture podatkov in topološko sestavo 2D-podatkov. 3D Geometry. Knjižnica zagotavlja trodimenzionalne geometrijske strukture podatkov in topološko sestavo 3D-podatkov. Topology. Topološka knjižnica omogoča zgradbe topoloških podatkovnih struktur. Topologija je definirana kot razmerje med enostavnimi in kompleksnimi geometrijskimi elementi. Omogoča sestavo kompleksih objektov in izdelavo objektov, ki so sestavljeni iz elementov različnih dimenzij. Knjižnica vsebuje orodja za določevanje lokacij poljubno izbranih oblik.

Algoritmi za modeliranje (ang. Modeling algorithms)

To je grupirana veriga topoloških algoritmov, ki se uporabljajo pri modeliranju. Modul vsebuje tudi algoritme za geometrijsko modeliranje. Modelirne algoritme uporabljamo s pomočjo že narejenih osnovnih oblik in operacij, s katerimi kombiniramo več različnih oblik. Med modelirne algoritme, s pomočjo katerih izdelujemo 3D-modele, štejemo: geometrijska orodja in pripomočke, topološka orodja, uporabo osnovnih oblik, Booleanove operacije, zaokrožitve in posnetja, odmikanje.

Mreženje prostora za prikazovanje (ang. Mesh)

Open CASCADE vsebuje funkcijo za mreženje objektov. Poleg mreženja vsebuje dva mrežna pretvornika: Pretvornik VRML prevede oblike OC v datoteke VRML 1.0 (VMRL - Virtual Reality Modeling Language). Pretvornik STL prevede oblike OC v format STL. Format STL (STtereo Litography) se pogosto uporablja za hitro izdelavo prototipov.

Predstavitev - vizualizacija (ang. Visualization)

Vizualizacija omogoča prikazovanje izbranih elementov oz. objektov, zato je njena glavna funkcija izbiranje in ločevanje podatkovnih vsebin. Vizualizacijo podatkovne strukture OC omogočajo algoritmi ready-to-use. Ti algoritmi izbrane podatke pripravijo za prikazovanje na zaslonu oziroma v zaslonskem prostoru. Omogoča prikazovanje celih 2D- in 3D-modelov in tudi poljubno izbranih delov poljubnega modela.

Standardizirana izmenjava podatkov (ang. Standardized Data Exchange)

Modul za izmenjavo podatkov v OC omogoča izmenjevanje podatkov OC z ostalimi programskimi paketi CAD. Izmenjevanje podatkov med modelirniki CAD je uporabno tudi v primeru, ko se model izdela v poljubnem modelirniku CAD. Tako ga lahko uporabljamo kot povezavo med raznimi programskimi paketi za inženirske analize in modelirniki. Model izdelka prepišemo v programski paket za statično analizo konstrukcije, nato pa rezultate prenesemo v modelirnik CAD. Model CAD se zapiše v standardni format (STEP/IGES) in uvozi v programski paket, ki že vsebuje module za izdelavo npr. statične analize. Najpogosteje se za izmenjevanje podatkov CAD med programi CAD uporabljata standardna formata STEP in IGES. STEP (AP203, AP214 in AP209) in IGES (5.3) omogočata pisanje in branje 3D-podatkov, kot so: 3D-geometrija in topologija, z dodatnim modulom XDE (ang. Extended Data Exchange) tudi izmenjavo barv in imen, strukture sestavov in plasti. Najpogosteje se za izmenjavo podatkov uporablja standard STEP, zato je v OC še posebno dobro razvit in podprt. Prednost formata OC STEP je še posebej prepoznavna pri prenosu geometrije kompleksnejših modelov. Modul OC STEP omogoča poleg zapisovanja in branja podatkov v formatu STEP tudi kakovostno analiziranje datotek STEP.

Aplikacijski programski okvir (ang. OC Application framework, skrajšano OCAF)

Modul OCAF vsebuje povezovalna orodja za poenostavitev razvoja in izdelave modelov CAD. Aplikacijska arhitektura vsebuje naslednje gradnike: manipulacija s podatki je zagotovljena z atributnim mehanizmom, atributi so organizirani glede na razvojne potrebe, aplikacijsko upravljanje večjih dokumentov, modeliranje podatkov ready-to-use v povezavi z aplikacijami CAD/CAM, podatkovni servis.

Organizacija dokumentov in podatkov je v modelirnikih ključnega pomena. V organizaciji se OCAF razlikuje od ostalih modelirnikov CAD. Podatkovna struktura ni razporejena glede na oblikovni ključ SKD (shape-key driven), ampak uporablja metodo referenčnega ključa RKD (reference-key driven). V primeru uporabe RKD so atributi, kot so oblika, barva, material in drugi, vključeni na nižje nivoje strukture, kot je določena sama oblika. Zaradi poglobljene podatkovne strukture s prej omenjenimi atributi se lahko v OCAF izvajajo manipulacije brez večjih težav. Poleg organiziranja podatkov nam OCAF omogoča tudi shranjevanje podatkov. Modul Data Storage s pomočjo knjižnice za shranjevanje podatkov zagotavlja zanesljivo shranjevanje podatkov na disk.

Grafični uporabniški programski okvir (ang. GUI framework)

Open CASCADE Graphical User Interface Framework (GUIF) je orodje za razvijanje uporabniškega vmesnika aplikacij, zasnovanih z Open CASCADE Application Framework (OCAF). Z uporabniškim vmesnikom GUIF se poenostavi in omogoči nekatere funkcionalnosti OC, in sicer: upravljamo več dokumentov na istem namizju; omogočeno je več različnih pogledov datoteke hkrati. Lahko pregledujemo kodo izbranega modela ob sočasnem prikazovanju istega modela; omogoča manipulacijo s 3D-modelom s pomočjo algoritmov ready-to-use: povečevanje, translacija, rotacija in grafično selektiranje poljubnega modela, dodatne uporabniške operacije so na poljubnih mestih dodane v pregledovalnikih.

OC GUIF je dostopen kot uporabniško orodje SALOME (SUIT), ki je del odprtokodne distribucije SALOME.

Razvojna orodja (ang. Development tools)

Open CASCADE vsebuje celoten sklop razvijalnih orodij, ki so primerni tako za posamezne razvijalce kode CAD kot tudi za uporabo pri večjih industrijskih projektih CAD. OC Test Harness ali Draw sta orodji, napisani v programskem jeziku C++ in namenjeni testiranju geometrijsko modelirnih knjižnic. Tako orodje omogoča testiranje in demonstracijo modeliranih komponent pred izdelavo celotne aplikacije. Sestavljeno je iz programskih podsklopov, in sicer: ukaznega interpreterja v jeziku TCL, 2D- in 3D-pregledovalnika, osnovanega na X v sistemih Unix in Win32 API v sistemih Windows, in sklopa preddefiniranih ukazov.

Slika 2. Zmogljivosti grafike Open CASCADE – modeliranje

WOK (Workshop Organization Kit) je podprogramski sklop, ki omogoča odpošiljanje enega ali več nizov strukturnih elementov programske kode velikih razvojnih projektov. Tak projekt je lahko sklop razvojnih podprojektov, ki jih nato razvijalci uporabijo za nadaljnji razvoj s standardnimi orodji in v sistemu organizacije različnih razvojnih timov v distribuiranih delovnih področjih. WOK omogoča prost dostop do standardnih nalog razvojnega procesa z raznimi orodji, kot so: urejevalniki (editorji), prevajalniki, povezovalniki (linkerji), iskalniki napak (debugerji) itd. Na sliki 2 je prikazan kompleksni 3D-model. Model je narejen s CAD-jedrom OC. Poleg izdelave omenjenih geometrij je v prikazovalniku predstavljena možnost zaslonskega izbiranja posameznih komponent.

Slika 3. Zmogljivosti grafike Open CASCADE – mreženje

Slika 3 prikazuje pomreženi 3D-model v OC. Po izdelavi mreže lahko naredimo analizo z MKE (metoda končnih elementov). Rezultate analize MKE nato v nadaljevanju prikažemo na istem modelu. Predstavitve so mogoče za različne parametre: napetosti, pomiki, temperatura z različnimi atributi.

Predstavitev CAD-jedra Open CASCADE na primerih

Predstavitev osnovnih ukazov OC na enostavnem 3D-modelu

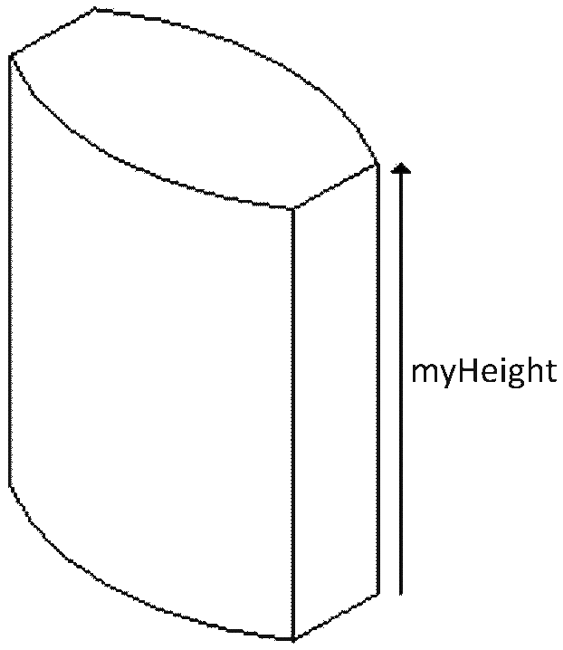
Na enostavnem primeru je prikazan postopek izdelave 3D-modela. Izdelava 3D-modela se začne na nivoju točk, nato pa se preko definiranja robov in uporabe funkcije za zrcaljene izvleče nastalo ravninsko površino v 3D-model. V nadaljevanju so prikazani ukazi za 3D-modeliranje z uporabo knjižnic Open CASCADE. Vsi zapisi bodo uporabljali programski jezik C++. Na sliki 4 je prikazan 3D-model, ki ga želimo izdelati. Model je orientiran glede na globalni kartezični koordinatni sistem XYZ, prikazan na sliki 4. Model je parametrično popisan z dimenzijami višine, dolžine in širine. Velikost parametrov modela: višina: myHeight = 70 mm, dolžina: myWidth = 50 mm,

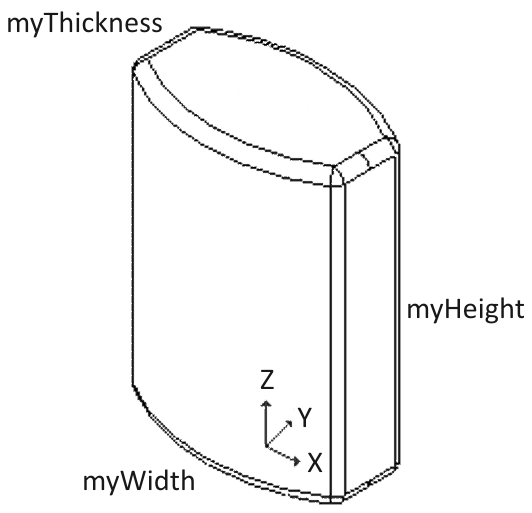
Slika 4. Dimenzijski popis 3D-modela

Algoritem izdelave enostavnega 3D-modela

Tvorjenje množice točk

Če želimo izdelati želeni 3D-profil, je potrebno v prvem koraku kreirati točke v ravnini XY0, ki ležijo na isti ravnini.

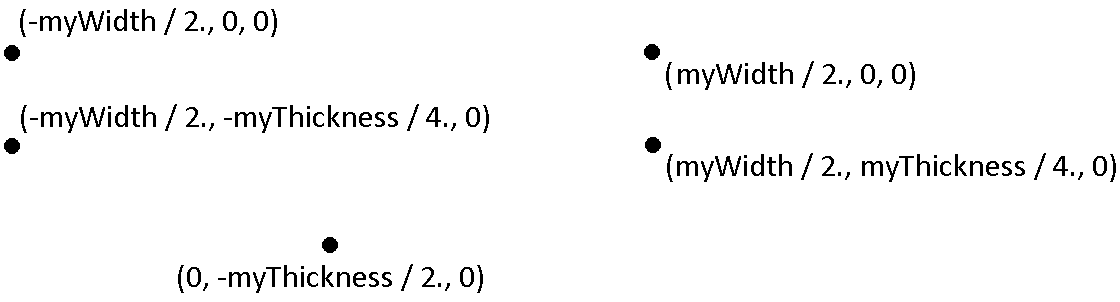
Slika 5. Sklop točk v ravnini XY

V OC obstajata dve možnosti za popis točke v kartezičnem koordinatnem sistemu: tvorjenje točke s primitivom gp_Pnt dinamična točka Geom_CartesiaPoint, ki je vodena s kazalcem handle

handle je kazalec, ki ima avtomatsko povezavo s spominom, v katerega se skladno z našo zahtevo zapisujejo podatki o trenutni lokaciji točke.

gp_Pnt je določen z izbrano vrednostjo in ima enako kot podobni objekti omejeno življenjsko dobo.

Geom_CartesianPoint je opredeljen glede na pozicijo handla, lahko je večkrat naslovljen in ima daljšo življenjsko dobo kot gp_Pnt. Vse točke so uporabljene le za pomoč pri tvorjenju krivulj za objekt omejene življenjske dobe. V našem primeru izberemo za kreiranje točk gp_Pnt objekt. Po izbiri gp_Pnt moramo definirati koordinate X, Y in Z v globalnem kartezičnem koordinatnem sistemu (slika 6).

Slika 6. Definiranje točk v ravnini (glej sliko 5)

Če se odločimo uporabiti za kreiranje objekta Geom_CartesianPoint, pa je sintaksa izdelave posamezne točke drugačna. Vsi objekti, zgrajeni s kazalcem handle, morajo uporabljati standarden C++ operator new. Podatki se zbirajo po principu, ki je prikazan na sliki 7. Grajenje objektov različnih velikosti je izvedeno na enak način.

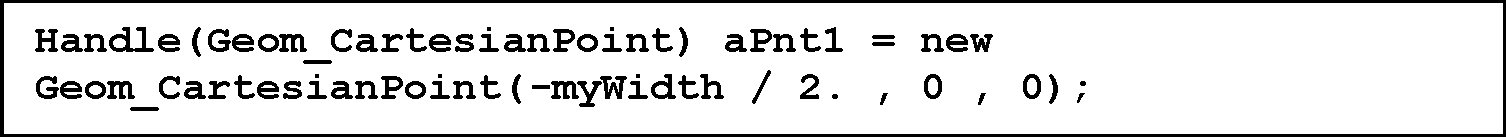
Slika 7. Uporaba ukaza handle za izdelavo točke

Če želimo v nadaljevanju programa prebrati podatke (npr. koordinate) o katerikoli izbrani točki v kartezičnem koordinatnem sistemu, lahko to opravimo na način, prikazan na sliki 8.

Slika 8. Prebiranje koordinat za posamezno točko

Povezovanje točk s krivuljami

Predhodno določene točke med sabo povežemo tako, da tvorijo geometrijo, sestavljeno iz dveh segmentov in enega loka, ki je napet med tremi točkami.

Slika 9. Prikaz posameznih krivulj med posameznimi točkami

Za risanje krivulj, prikazanih na sliki 9 moramo v programsko kodo vključiti trodimenzionalne geometrijske objekte, ki se nahajajo v paketu OC Geom. Za vse vrste krivulj (npr. daljica je krivulja) uporabimo specifičen ukaz. V našem primeru za izdelavo segmenta (ravna linija – daljica) uporabimo objekt GC_MakeSegment. Segment se izdela tako, da določimo dve robni točki P1 in P2 in za povezavo med njima določimo ravno linijo. Za objekt po sliki 9 moramo povezati oba konca segmentov s krivuljo, ki je določena s tremi točkami. Izbor zaporednih ukazov za posamezne geometrijske elemente, to je dveh segmentov in loka, je prikazan na sliki 10. Obe funkciji za izdelavo krivulj uporabljata ukaz handle Geom_TrimmedCurve.

Slika 10. Izdelava posameznih elementov, v splošnem krivulj med izbranima točkama

Slika 11. Ukaz za preverjanje možnosti izdelave krivulj med dvema točkama

V primeru, da se pred risanjem izbrane krivulje želimo prepričati o možnosti izdelave krivulje, uporabimo ukaza isDone in Value. Uporaba obeh ukazov je predstavljena na primeru kreiranja segmenta po sliki 11.

Definiranje podatkovne topološke strukture

Do sedaj smo narisali tri krivulje, njihova povezanost ni v ničemer določena. Povezanost med njimi določimo s topološkim popisom. Topologijo lahko izvajamo ločeno, korak za korakom ali pa s skupinskim ukazom. Če želimo poenostaviti modeliranje, je potrebno narisane krivulje združiti v eno samo. Združevanje izvedemo s podatkovno topološko strukturo OC, tako da uporabimo sklop ukazov paketa TopoDS. Ukazi TopoDS vsebujejo definicijo med geometrijskimi entitetami, ki so lahko združene. Objekti, ki jih določimo s pomočjo sklopa ukazov TopoDS, so prikazani v spodnji tabeli.

Oblika =	= Open CASCADE objekti =	= Opis =
Vertex	TopoDS_Vertex	Brezdimenzionalna oblika, ki ustreza geometriji točke
Edge	TopoDS_Edge	Enodimenzionalna oblika, ki ustreza krivuljam in je omejena na robovih
Wire	TopoDS_Wire	Niz robov, povezanih z vozlišči
Face	TopoDS_Face	Površina, omejena z zanko
Shell	TopoDS_Shell	Sklop površin, povezanih z robovi
Solid	TopoDS_Solid	Kos v 3D-prostoru, omejen z lupino
CompSolid?	TopoDS_CompSolid	Sklop 3D-teles, povezanih s površinami
Compound	TopoDS_Compound	Sklop katerihkoli oblik

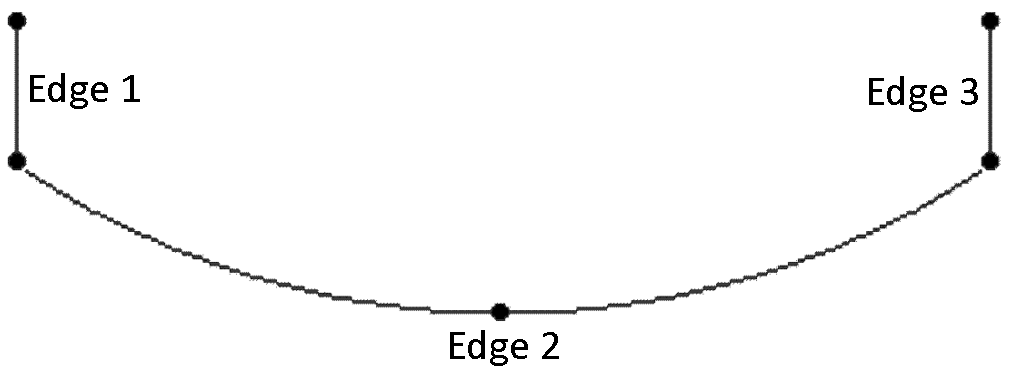
Slika 12. Prikaz izdelave elementov robov (Edge)

Posamezne izrisane krivulje združimo glede na ukazje po tabeli 1 tako, da dobimo tri robove, ki so med seboj povezani (slika 12), zato jih omenjeni ukazi tudi označijo ter atribute zapišejo v bazo podatkov. Ukazni sklop TopoDS določa le podatkovno topološko strukturo elementov. Algoritmi za izračun standardnih topoloških elementov se nahajajo v paketu BrepBuilder? API. Za izdelavo roba se uporabi objekt BRepBuilderAPI_MakeEdge z že določenimi krivuljami.

Slika 13. Opredelitev topološkega elementa (rob, ang. Edge) iz krivulj

V OC je poleg izdelave robov s preddoločenimi krivuljami mogoča tudi izdelava robov neposredno s pomočjo določitve posameznih točk. Omenjeni način pa velja samo za izdelavo ravnih krivulj med dvema poljubnima točkama.

Slika 14. Ukaz za določanje robov neposredno iz izbranih točk

Mreženje skupine robov

1) Mreženje skupine robov, ki je odprto

V skupini robov, ki so topološko med seboj določeni, lahko njihove povezave strnemo v mrežo. Mreža robov je lahko odprta ali zaprta. Izdelamo jo na dva načina, in sicer: neposredno, če izdelujemo mrežo iz enega do štirih robov; z dodajanjem in združevanjem več mrež, ki so sestavljene iz enega do štirih robov.

Za izdelavo mreže se v primeru treh robov uporabi neposredno metodo izdelovanja mreže, ki je prikazana v naslednji formi C++:

Slika 15. Ukaz, s katerim iz opredeljenega števila robov določimo mrežo, ki je topološko opredeljena

2) Mreženje skupine robov, ki je zaprto

Robove, ki so povezani med seboj tako, da so v zaprti zanki, lahko uporabimo za različne namene. Najpogostejša uporaba je izvlek, ki fizično lahko opredeljuje različne profile (npr. U, I ipd.). Tako dobimo zelo hitro različne 3D-modele profilov, ki jih v vsakdanjem življenju najpogosteje uporabljamo. Najlažji način za izdelavo zaprtega profila je, da določen rob ali skupino robov prezrcalimo in nato prezrcaljeni rob ali skupino robov pridružimo prvotni mreži profila.

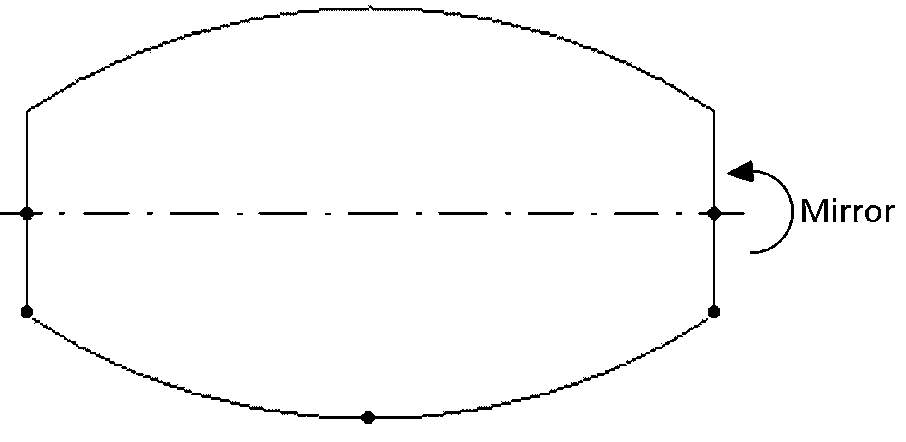
Slika 16. Izdelava zrcalne slike prvotno definiranega lika. Označimo rob in določimo os zrcaljenja. [BR]]

Pred procesom zrcaljenja pa moramo opredeliti širši prostor, v katerem bomo nato uporabili 3D-transformacije. V ta namen vključimo modul za trodimenzionalno geometrijsko transformacijo (gp_Trsf). Omenjeni modul vsebuje značilne funkcije transformacij, kot so translacija, rotacija, skaliranje, zrcaljene itd., in omogoča različne kombinacije med njimi. V našem primeru se osredotočimo na zrcaljene okrog osi X globalnega koordinatnega sistema XYZ (glej sliko 4).

Os X, okoli katere bomo izvajali rotacijo, lahko določimo na dva načina: 1) točka P1 in smer vektorja, ki poteka skozi točko P1, 2) s posebnim ukazom za določitev osi X.

1) točka P1 in smer vektorja, ki poteka skozi točko P1 os X poteka skozi točko P1(0, 0, 0) – uporabimo ukaz gp_Pnt smer osi X določa enotski vektor (1, 0, 0) – uporabimo ukaz gp_Dir

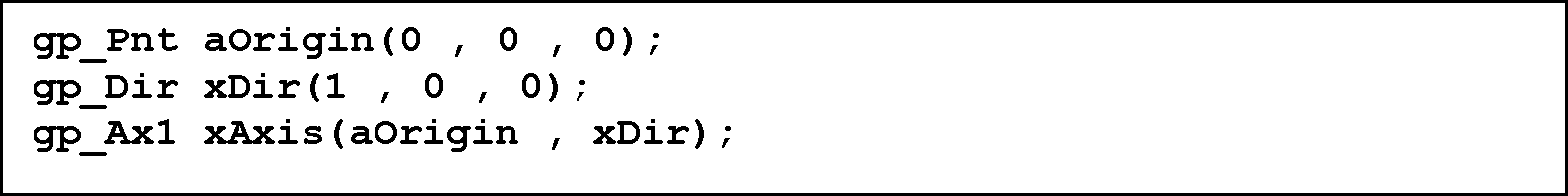
Slika 17. Opredelitev potrebnega števila spremenljivk, ki omogoča določitev osi X

2) opredelitev osi X v prostoru z neposrednim ukazom

Slika 18. Ukaz za neposredno določitev osi X, ki pa je osnovana na vnaprej določenem oz. aktualnem koordinatnem sistemu
Če želimo izvajati zrcaljenje okoli prej opredeljene osi X, v nadaljevanju uporabimo zrcalno metodo SetMirror?.

Slika 19. Opredelitev zrcalne osi in njene spremenljivke
Sedaj imamo vse parametre, ki jih potrebujemo za izvedbo zrcaljenja mreže robov okrog osi X. Za samo zrcaljenje pa uporabimo ukaz, ki vsebuje argument zrcaljene geometrije in podatke o osi, okrog katere izvedemo zrcaljenje.
Imag(slika15-20.png, width=480px,align=center)?
Slika 20. Ukaz za procesiranje zrcaljenja po prej določeni osi X, okoli katere se zrcaljenje izvede
Funkcija BrepBuilderAPI_Transform ne spreminja narave zrcaljene oblike, zato smo dobili poleg zrcalne slike mreže tudi samo mrežo robov. Da vrnemo mrežo robov nazaj, moramo uporabiti reverzno funkcijo oziroma ukaz BrepBuilderAPI_Transform::Shape, ki vrne objekt TopoDS_Shape v prvotno lego.

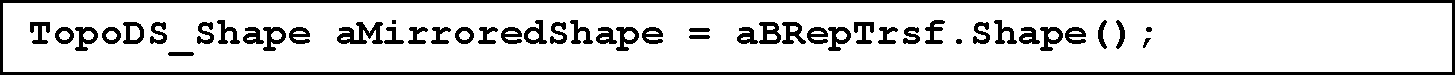
Slika 21. Ukaz za reverzno funkcijo, ki mrežo robov povrne v zrcalno geometrijo Shape

Sedaj imamo dve mreži robov. Ena je osnovna, druga pa zrcaljena v enem delu. Da lahko začnemo sestavljati novo mrežo robov, moramo najprej stare povezave, določene s staro topologijo, prestaviti v skupino krivulj. Za tako operacijo uporabimo sklop ukazov TopoDS. Z ukazom TopoDS::Wire tako vrnemo mrežo robov v skupino krivulj.

Slika 22. Ukaz za formiranje topološkega zapisa mreže robov, ki ga izvedemo iz nedoločeno povezane mreže robov


Slika 23. Združitev prvotne in zrcalne mreže
Sedaj imamo skupino krivulj, ki jo moramo povezati v mrežo robov. Ker so robovi med seboj povezani, dobimo zaključeno oziroma zaprto mrežo robov ali enostavno zanko. Za tako operacijo uporabimo ukaz BrepBuilderAPI_MakeWire. Najprej določimo naziv za mrežo, nato pa pod tem imenom vpisujemo zaporedno od prvega roba do zadnjega in tako ustvarimo zaprto mrežo oziroma zanko.

Izdelava prizme iz zanke robov (zaprta mreža robov)

Prizmatično telo izvedemo tako, da taki zanki robov pridodamo v določeni smeri parameter višine. Parameter višine je pravokotna razdalja med izhodiščno zanko robov in zanko robov, ki je druga ploskev prizme. Za tako operacijo uporabimo ukaz Prism. V ukazu privzamemo zanko robov kot izhodiščni lik in smer premikanja lika do določene višine h.

Tabela: Povezava med gradniki in elementi

= Oblika =	= Generira =
Vertex	Edge
Edge	Face
Wire	Shell (Loop)
Face	Solid
Shell	Compound of Solid

Slika 24. Prikaz 3D geometrije izvedene s funkcijo izvleka
V računalniški terminologiji se velikokrat za enake fizikalne predstavitve ali procese uporablja več različnih izrazov. Tudi v našem primeru je pri uporabi pojma Shell (Loop) potrebno razumeti, da je to v bistvu zanka. Zanka je zaključena mreža robov, ki v geometriji dejansko predstavlja lik. Pogoj za to je, da vsi robovi in točke ležijo v isti ravnini. V opisanem programu OC se pojavljata pojma, ki sta opredeljena kot mreža robov (odprta zanka) ali zaprta mreža robov (zaprta zanka). Opozorilo o različnih terminih smo dodali zato, da bo dodaten študij programa OC lažji in ne zavajujoč. Na začetku predvidene operacije imamo samo zanko robov, zato moramo najprej opredeliti površino osnovnega lika. Za opredelitev površine uporabimo poseben ukaz BrepBuilderAPI_MakeFace. Kot smo že povedali, je površina sestavljena iz zaključene mreže robov, to je zanke. Če vse točke in celotna zanka robov ležijo na isti ravnini, se lahko ukaz za izvlek uporabi neposredno.

Slika 25. Ukaz, ki opredeli zanko robov kot površino. Na ta način dobimo iz enega topološkega elementa drugi višji topološki element
Podprogrami BrepBuilderAPI omogočajo izdelavo topoloških primitivov konstrukcij, kot so škatle, stožci, valji, krogle itd. V tej skupini podprogramov je tudi ukaz za izdelavo prizme BrepPrimAPI_MakePrism. Za uporabo tega ukaza potrebujemo naslednja parametra: 1) osnovni lik, ki je določen s površino in 2) smerni vektor, v smer katerega se izdela izvlek osnovne oblike. Smerni vektor za izdelavo prizme v smeri površinske normale na določeno višino prizme je določen z ukazom myHeight:

Slika 26. Ukaz za določitev vektorja izvleka, ki je v tem primeru pravokoten, glede na osnovno površino
Na osnovi obeh parametrov lahko s sklepnim ukazom izvedemo model prizme. Zato uporabimo ukaz BrepPrimAPI_MakePrism, ki določi vse topološke podatke za prizmo, ki tako postane trdno telo.

Slika 27. Določitev naslednjega topološkega elementa, trdno telo, to je naš 3-D model

Zaokroževanje robov

Ker so robovi nastale prizme ostri, jih želimo zaokrožiti. Za zaokroževanje robov se uporabi v OC ukaz Fillet (zaokroževanje). V našem primeru zapleteno zaokroževanje robov poenostavimo na način, da so vsi robovi enako zaokroženi s polmerom myThickness/12 (glej sliko 28).

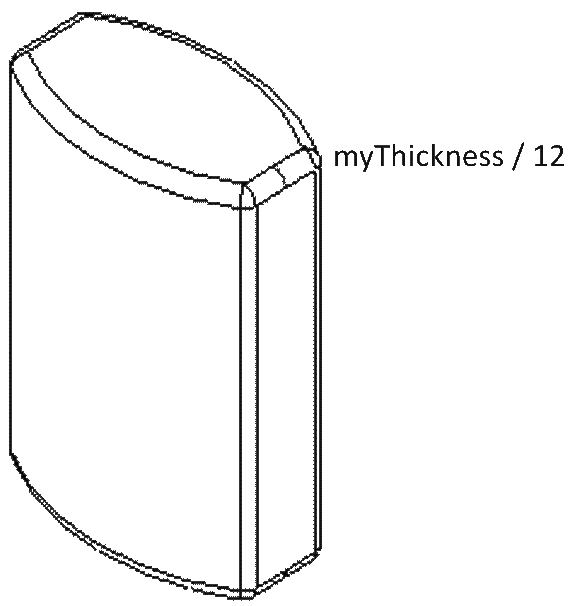
Slika 28. 3D model z zaokroženimi robovi
Za izvajanje zaokroževanj (Fillets) robov na poljubnih 3D-modelih lahko uporabimo sklop ukazov BrepFilletAPI_MakeFillet. Različne ukaze uporabljamo na naslednji način: v sklopu ukazov BrepFilletAPI_MakeFillet (kot neke vrste konstruktor) določimo 3D-model, kateremu želimo zaokrožiti robove; nato določimo skupino robov, ki jih želimo zaokrožiti. Pri tem vedno uporabljamo skupino robov, ki imajo enake zaokrožitve, zato moramo najprej določiti polmer zaokrožitve. Robove, ki jih bomo zaokrožili, pa bomo dodajali z ukazom Add; po izvedenih ukazih stalno spremljamo, kakšne oblike telesa se pojavijo za vsak rob posebej.

Slika 29. Ukaz za aktiviranje zaokroževanja
Prav pri zaokrožitvah se velikokrat pojavi zahteva po dopolnjevanju ali spreminjanju podatkov. Zato moramo uporabiti funkcijo prikazovanja podatkov na zaslonu neposredno. Z namenom, da imamo podatke predstavljene na zaslonu in jih nato po potrebi spreminjamo, uporabimo ukaz TopExp_Explorer, ki pregleda zapisane podatke o izbranem modelu in nam vrne klicane parametre:

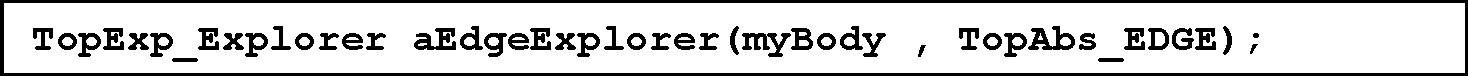
Slika 30. Izpisovanje podatkov o zaokroženih robovih
Raziskovalec (Explorer) je vgrajen v zanko in uporablja tri glavne metode: More – poizvedba o podmodelih (sub-shapes), ki jih mora še raziskati; Current – potrebno je vedeti, v katerem podmodelu se nahajamo; Next – premik na naslednji še neraziskani podmodel.

Slika 31. Za iskanje robov v 3-D modelu uporabljamo while zanko
S pomočjo raziskovalne zanke (explorer loop) lahko odkrijemo vse robove na izbranem modelu. Če želimo posamezni rob pridodati v nabor zaokroženih robov, to izvedemo z ukazom za dodajanje Add v ukaznem sestavu BrepFilletAPI_MakeFillet. Poleg podatka o zaokroženem robu moramo določiti še polmer zaokrožitve robov:

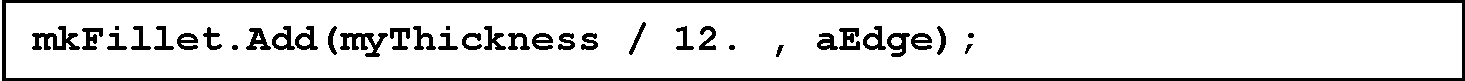
Slika 32. Ukaz za določitev polmera zaokrožitve za skupino robov


Slika 33. 3D model z izpisanimi vrednostmi zaokrožitev na robovih (vse zaokrožitve na modelu so myThickness/12)
Po zaporednem določanju robov in polmerov zaokrožitev nato z zadnjim ukazom postavimo zahtevo za eksekutivno izvedbo oblike za vse izbrane robove. Na ta način zapišemo vse zaokrožene oziroma spremenjene površine v bazo podatkov za obravnavano trdno telo.

Slika 34. Vpis spremenjenih (zaokroženih) površin v bazo podatkov za obravnavano trdno telo v jeziku C++
Z uporabo zadnjega ukaza imamo v bazi podatkov vse podatke in zapisano topologijo. S primerom smo poskušali predstaviti generiranje relativno enostavne oblike, ki pa v končni obliki postane zelo kompleksen model. Razumljivo je, da tako enostavnih oblik v naravi praviloma ni. Prav v tem pa se izkaže prednost OC. Če namreč pri komercialno uporabnih modelirnikih določene zahtevnejše oblike ne moremo zanesljivo določiti v vseh detajlih, pa z uporabo OC lahko dobimo bistveno natančnejši popis oblike tudi pri najzahtevnejših prostih površinah. V knjigi je predstavljen zelo zožen nabor ukazov. V knjižnici je bistveno več ukazov, ki si jih uporabnik lahko dodatno ogleda in uporablja.

Izdelava 3D-modela vozlišča jeklene konstrukcije

Izdelava CAD-modela vozlišča jeklene konstrukcije je prikazana na primeru izdelave nosilnega vozliščnega elementa v poljubni mrežni strukturi, prikazani na sliki 35. Pri predstavitvi bomo uporabljali programski jezik C++ in odprtokodno CAD-jedro Open CASCADE (OC). Odločitev za uporabo OC je bila v tem primeru osnovana na zahtevi popolnega prosto površinskega modela, ki bi bil generiran v posebnem generatorju oblik, nato prenesen v inženirski model za analizo napetostnih stanj, zatem pa preverjan glede na detajlno obliko v vozliščih, ki bi se v končni uporabi prenesli v mikrookolje za končno varjenje vozliščnega sklopa v robotiziranih sistemih. Omenjeni model CAD je potrebno izdelati za poljubne mrežne točke, ki se nahajajo v prostoru in imajo različno orientacijo. Vsaka točka mrežne strukture je povezana z najmanj tremi točkami. Poudarjamo, da je bilo prav zaradi kompleksnosti problema uporabljeno CAD-jedro OC, ki omogoča izdelavo splošnega modela in ga bo mogoče izdelati za poljubno mrežno strukturo.

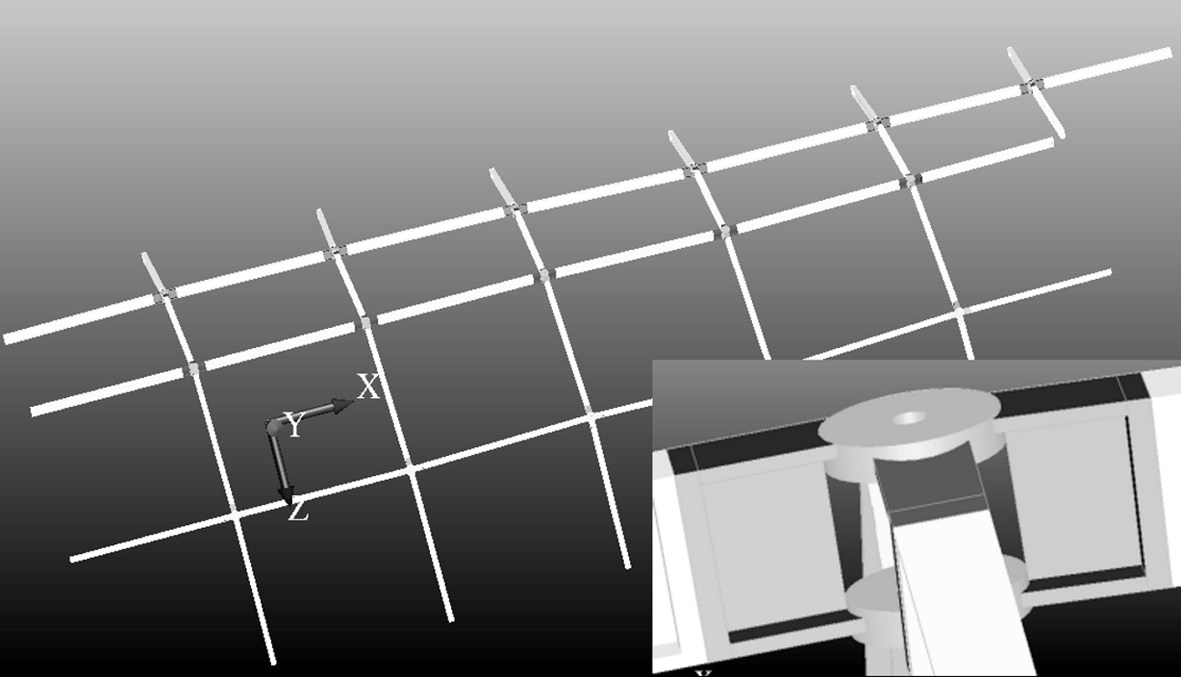
Slika 35. Mrežna struktura CAD in vozliščni element
Primer, ki ga obravnavamo, je predstavljen zato, da lahko potrdimo možnost celotnega procesa razvoja, inženirske analize, konstrukcije, izdelave, transporta, montaže in finalne uporabe. Pri tem je bil razvit poseben program, ki omogoča spremljanje vseh faz procesa zato, ker je v celoti določena geometrija in so sprotno obvladljivi vsi podatki, potrebni za kakršnekoli analize in določanja oblike. Zaradi povečane hitrosti procesiranja je bila prednost takega pristopa izkazana že v treh ponovljenih izvedbah. Na sliki 35 je prikazan mrežni model CAD, izdelan s programskim jezikom C++ in CAD-jedrom OC. Mrežni model je izdelan iz poljubne vhodne mrežne strukture, ki je sestavljena iz petnajstih vozlišč. Za vsako vozlišče bomo glede na orientacijo posameznega vozlišča izdelali cilindrični vozliščni element, na katerega se varijo oziroma po potrebi vijačijo I-profili, ki jih modeliramo v poenostavljeni obliki.

Slika 36. 3D model vozliščnega elementa
V nadaljevanju bomo predstavili zaporedje glavnih funkcij oz. operacij v OC ter izpeljane ukaze za izdelavo tako zastavljenega modela oziroma konstrukcije. Postopek za modeliranje posameznega elementa z izvlekom je predstavljen v prejšnjem poglavju, zato se pri izdelavi CAD-modela vozlišča osredotočimo predvsem na novo uporabljene funkcije.

Izdelava CAD-modela vozlišča

Zaradi povezanosti programa bomo tudi v tem primeru predstavili postopek, ki bo zapisan v programskem jeziku C++.

Kreiranje praznih sestavov

Poimenovanje posameznih praznih pomnilnih prostorov uporabimo zato, da jih lahko kasneje pokličemo za neposredno ločeno prikazovanje. V njih se shranjujejo posamezne pozicije, to so izdelki sestava CAD-modela vozlišča.

V spremenljivko aResVertex se shrani sestav cilindričnega vozlišča. Spremenljivka aResI je rezervirana za poenostavljene vozliščne I-profile. Profile v nadaljevanju s pomočjo Booleanove operacije razlike odrežemo s plaščem cilindra vozlišča in shranimo v novo spremenljivko aResI_cut.

Slika 37. Priprava oziroma rezervacija raznih spremenljivk vozliščnega elementa

Izdelava profilnih elementov v vozlišču (točke, robovi, mreže, zanka, površina)

Na začetku določimo pozicijo točk v prostoru, ki bodo sestavljale prerez poenostavljenega vozliščnega I-profila. Za popis prereza poenostavljenega I-profila potrebujemo dvanajst točk aPnt1, …, aPnt12, ki jih razporedimo glede na vozlišče mrežne strukture in se nahajajo na isti ravnini. Poudarjamo, da je upoštevano, da je prerez v isti ravnini. Pravimo, da je prerez je planaren.

Slika 38. Definiranje točk vozliščnega profila v prostoru
V nadaljevanju določimo robove vozliščnega elementa, ki so odvisni od dimenzij I-profila.

Slika 39. Ukaz za izdelavo robov iz posameznih točk
Predstavljene točke moramo združiti v linijske robne elemente, ki jih v nadaljevanju uporabimo za tvorjenje mreže robov, nato v zaprte mreže robov oz. zanke, površine in na koncu po izvajanju izvleka opredelimo še pravi 3D-model. Iz robov myEdge1 … myEdge12 v nadaljevanju tvorimo mrežo myWire1 … myWire3. Ker lahko v eno mrežo vključimo največ štiri robove, je potrebno izdelati tri mreže, ki jih združimo (Add) in ustvarimo eno mrežo z imenom myWire, kakor je prikazano na sliki 40.

Slika 40. Ukaz za izdelavo posameznih in skupne mreže robov
Zaprto mrežo robov ali zanko v nadaljevanju uporabimo za določitev površine myFace. Ko je površina osnovne ploskve (ali bolje osnovni lik) določena, lahko izvedemo njen izvlek s pomočjo smernega vektorja vector, ki ga izračunamo glede na začetno in končno točko dolžine realnega I-profila. Tako dobimo 3D-model I-profila, ki ga opredelimo z ukazom myShape.

Slika 41. Ukaz za izvlek osnovne površine, ki ima določeno dolžino vector, za opredelitev 3-D modela realnega I-profila

Rezanje profilnih elementov

Vozliščni element v realnem svetu predstavlja določen premer valja, ki ima središčno os enako, kot je središčni vektor vozlišča. Da lahko opredelimo ravnino, kjer se I-profil v dotiku z valjem vozliščnega elementa konča, moramo najprej opredeliti ravnino, ki je tangencialna na valj vozliščnega elementa. Ne pozabite, da ves čas razumemo, da je vozliščni element postavljen v 3D-prostoru. Zaradi postopka moramo najprej določiti valj vozliščnega elementa (slika 42).

Slika 42. Določitev glavnih podatkov za izdelavo valja vozliščnega elementa


Slika 43. Izdelava 3-D modela valja vozliščnega elementa

V prvem delu (slika 43) kode določimo pozicijo, smer in premer valja, ki ga generiramo kot del vozliščnega elementa. Nato pa v nadaljevanju odrežemo že generirane I-profile od po sliki 43 generiranega valja vozliščnega elementa. Ukaz za Booleanovo operacijo je predstavljen na sliki 44.

Slika 44. Booleanova operacija , ki določi razlike med valjem in vozliščnimi profili

Posebej moramo opozoriti, da vozliščni I-profil myShapeI ne poteka natančno do mrežnega vozlišča, ampak samo do prirobnice, ki jo predstavlja sedaj generirani valj vozliščnega elementa. Zaradi tega moramo I-profil odrezati na razdalji zunanjega roba cilindričnega vozlišča z ukazom cylinderCut. Operacijo odrezovanja izvedemo s pomočjo Booleanove operacije razlike. Od izbranega elementa I-profila odštejemo vozliščno geometrijo s funkcijo BrepAlgo_Cut. Takoj za izvedeno operacijo nato preostanek oziroma odrezani I-profil shranimo v sestav aResI, ki smo ga opredelili na samem začetku. To izvedemo z uporabo ukaza AddAIS_Shape, ki pa nam omogoči tudi prikazovanje rezultata v želeni barvi.

Izračun oddaljenosti središča prvega I-profila (prvega sestavnega dela) modela vozlišča CAD od vozlišča mrežne strukture v smeri vozliščne normale

Za skrbno določitev prostorske postavitve vseh delov sestava našega vozlišča, to je I-profilov in samega vozliščnega elementa, moramo določiti za vsak I-profil njegovo oddaljenost od centralne osi vozlišča mrežne strukture jeklene konstrukcije. Posebej poudarjamo, da je vsako vozlišče mrežne strukture jeklene konstrukcije postavljeno različno v globalnem koordinatnem sistemu, torej niti eno ni enako pozicionirano. Pri tem imamo pred seboj tako vse tri koordinate globalnega koordinatnega sistema kot tudi kote in značilne za usmeritev lokalnega koordinatnega sistema v primerjavi z globalnim. Zaradi tega moramo s posebnim programom določiti lokalni koordinatni sistem za vsako vozlišče mrežne strukture jeklene konstrukcije posebej.

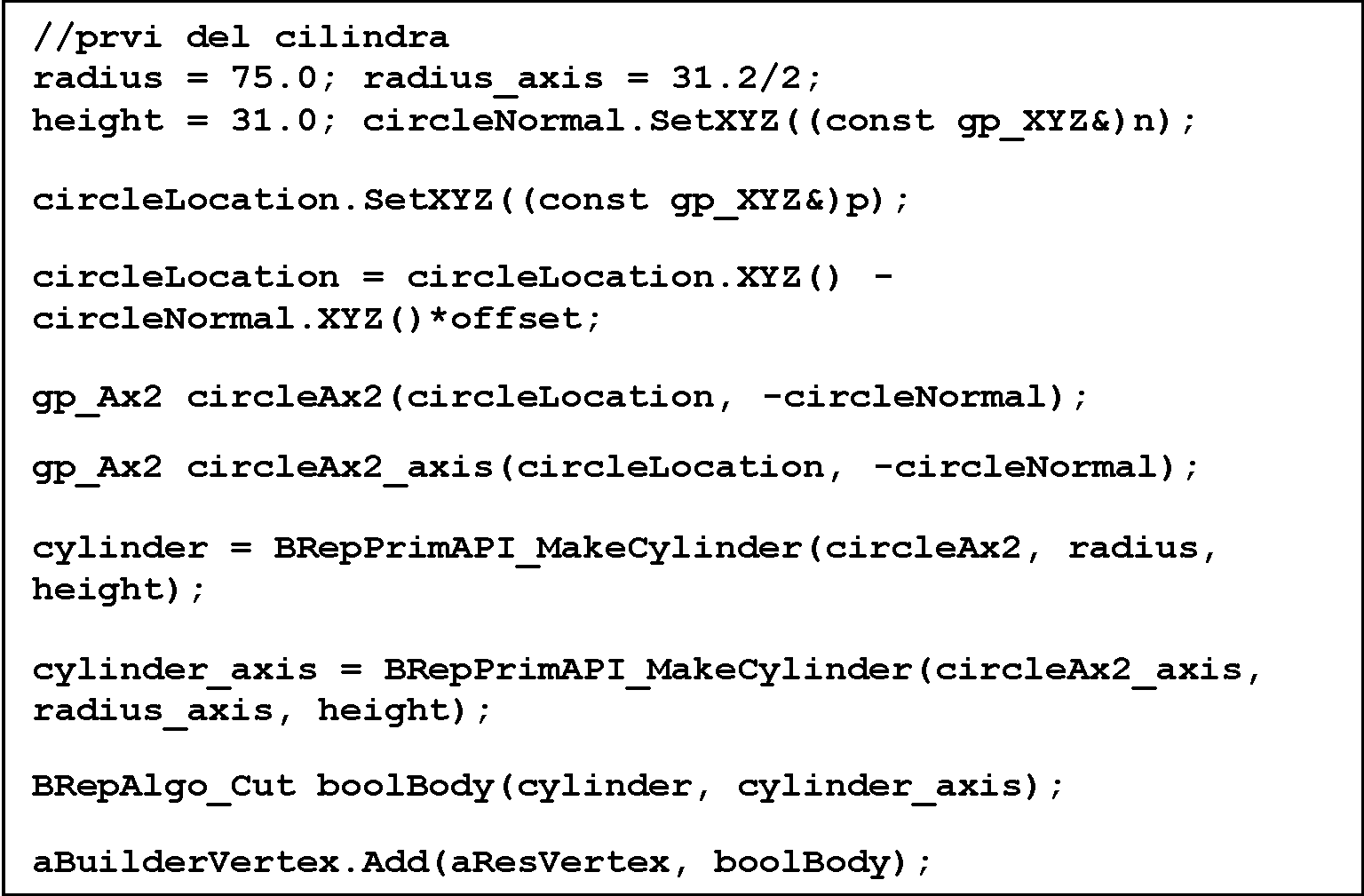
Slika 45. Izdelava zgornjega dela valja vozliščnega elementa

Določitev vozliščnih parametrov (smer, razdalja, sestavni deli)

Valj vozliščnega elementa ima določene dimenzije, ki jih moramo določiti vnaprej. Vnos podatkov je postopen in v bistvu parametričen. Če so določene dimenzije znane, pa jih vnašamo kar z dejanskimi vrednostmi. Parameter oz. spremenljivka radius (slika 45) določa polmer cilindra, ki je 75 mm. S spremenljivko radius_axis se popiše polmer srednje izvrtine v valju, višino valja določa spremenljivka height z 31 mm. Izvrtino v večji valj se naredi z uporabo Booleanove operacije razlike BrepAlgo_Cut. Po opredelitvi valja, ki še nima določene lokacije v prostoru, pristopimo k opredelitvi izhodiščne točke oziroma njene umestitve v lokalnem koordinatnem sistemu, z definiranjem spremenljivke circleLocation (glej sliko 45).

Slika 46. C++ koda izdela vmesni del valja vozlišča
Drugi del sestava vozliščnega elementa vozliščnega cilindra je osrednji (ožji) del. Določimo ga tako, da najprej določimo premer srednjega dela cilindra, ki ga popisuje spremenljivka radius z dimenzijo 21,2 mm. Višina valja je 109 mm in jo lahko programsko vpišemo kot spremenljivko height. Tako določenemu in poimenovanemu srednjemu delu vozliščnega elementa nato s pomočjo Booleanove operacije razlike izvrtamo skoznjo izvrtino premera 31,2 mm (pazite, to je polmer 15,6 mm!). Zgornji del srednjega dela vozliščnega elementa priključimo spodnji površini zgornjega vozliščnega elementa takrat, kadar sta centrični glede na isto srednjico. Poudarimo naj, da spodnja površina velikega valja (prvi, ki smo ga generirali) leži na zgornji površini srednjega dela, to je drugega valja.

Slika 47. Zaporedje ukazov za modeliranje tretjega valja, ki j oblikovno enak prvemu delu


Slika 48. C++ koda z uporabo OC funkcij izdela STEP/IGES format CAD modela


Slika 49. STEP (levo) in IGES (desno) modela vozlišča generirana v Open CASCADE in uvožena v ProEngineer? Wildfire 3.0
Na sliki 49 imamo predstavljen model CAD našega vozliščnega elementa z vsemi priključenimi I-profili, ki je uvožen v formatu STEP/IGES v ProE Wildfire 3.0. Na ta način dokazujemo splošno uporabnost takega nevtralnega formata.

Izdelava modela CAD I-profila

Z namenom, da predstavimo pomembne prednosti modeliranja v programskem okolju OC, bomo v nadaljevanju predstavili model CAD poenostavljenega I-profila, ki je bil izdelan s programskim jezikom C++.

Slika 50. Poenostavljeni I-profili, ki med sabo povezujejo vozliščne elemente
Slika 50 prikazuje model CAD poenostavljenega I-profila. Predstavljeni elementi I-profilov so odrezani glede na zunanjo površino cilindričnega vozlišča. V nadaljevanju je predstavljen algoritem poteka izdelave modela CAD poenostavljenega I-profila.

Izbira poljubnega roba ali celotne mrežne strukture

Opredelitev praznega sestava

Ta postopek je obvezen pred vsakim definiranjem geometrije in zagotavlja ustrezno pomnilno kapaciteto za vsak poimenovani sestav.

Slika 51. Ukaz za shranjevanje v spomin posameznih I-profilov, kot elementov CAD modela
Predvideni sestav ima ime aResI, ki ga izberemo in omogoča shranjevanje podatkov za I-profile.

Določitev dolžine I-profila

Pri narisanem I-profilu preberemo začetno in končno točko na isti tvornici (lahko srednjici) profila. Lahko pa določimo dolžino profila sami z vnaprejšnjim določanjem izhodiščne točke in vektorja dolžine. Glede na podan rob eh določimo začetno from in končno to točko izbranega profila.

Slika 52. Ukazje za določitev začetne in končne točke izbranega profila

Določitev normale za izbrani rob

Izbranemu robu določimo normalo n, ki jo uporabimo za določitev usmerjenosti I- profila v prostoru.

Slika 53. Ukaz za izračun robnih normal

Tvorjenje robnih točk poenostavljenega I-profila (glej sliko 48)

Prerez v splošnem popišemo najmanj s tremi točkami. Število točk za popis posameznega prereza določa njegova zahtevnost oziroma naša zahteva po natančnosti popisa. I-profil v našem primeru poenostavimo in ga popišemo z dvanajstimi točkami (glej sliko 48). Točka a.XYZ() določa tudi začetek I-profila. Začetna točka a nam omogoča opredelitev celotnega prereza ter njegovo lokacijo v prostoru, saj je točka a izhodiščna točka. Razdalja startI predstavlja odmik profila od začetne vozliščne točke mreže vozlišč jeklene konstrukcije v smeri robne normale normal.XYZ(). Glavne dimenzije prereza določamo s širino I- profila in jo določa parameter widthI1. Parameter widthI1 je usmerjen v smeri pravokotno na normalo roba normal2.XYZ(). Širino pasnice istega poenostavljenega I-profila popisuje parameter lengthI1.

Slika 54. Določitev pozicije točk prereza poenostavljenega I-profila

Tvorjenje robov iz robnih točk poenostavljenega I-profila

Na osnovi podanih točk aPnt1…aPnt12 lahko opredelimo skupino robov myEdge1…myEdge12. Zaprta mreža ali zanka robov predstavlja lik oziroma prerez poenostavljenega I-profila.

Slika 55. Iz znanih točk določimo robove in zanko robov za določitev osnovnega lika

Tvorjenje mreže robov (zanke) iz robov prereza

Če želimo opredeliti zaprto mrežo robov (zanke) iz robov prereza, moramo robove myEdge1…myEdge12 združiti. Omenjene robove smo opredelili z ukazi po sliki 53. Najprej izvedemo združevanje v mreže myWire1…myWire3, ki jih v naslednjem koraku združimo z ukazom Add v skupno mrežo myWire.

Slika 56. Iz robov C++ koda izdela posamezne in skupno mrežo

Določitev površine prereza in modela CAD poenostavljenega I-profila

Po opredeljeni mreži oziroma zanki z imenom myWire preverimo še, ali točke in robovi ležijo v isti ravnini, torej so na površini, ki je planarna. Če je ta pogoj izpolnjen, lahko izvedemo ukaz za določitev površine myFace. Opredeljeno površino nato izvlečemo v smeri normale na ravnino in dobimo model CAD poenostavljenega I-profila. Operacijo izvleka izvedemo tako, da iz ravninskega lika ustvarimo 3D-prizmo, kar smo že večkrat prikazali. Smer površine določa normalni vektor myVector, ki kaže v smeri normale na rob in je po razdalji enak dolžini roba profila.

Slika 57. Določitev smernega vektorja izvleka profila in izdelava 3-D elementa

Izvoz formata STEP /IGES modela CAD poenostavljenega I-profila in uvoz formata STEP/IGES v ProE Wildfire 3.0

Za izvoz v format STEP ali IGES moramo vsakemu I-profilu najprej nastaviti plast profila. Šele nato ga lahko izvozimo v nevtralni format STEP ali IGES. Ukaz za določanje plasti in geometrije profilov je Profile.

Slika 58. Ukaz za prenos podatkovne strukture iz OC v nevtralni format STEP/IGES format


Slika 59. STEP (levo) in IGES (desno) modela I profila generirana v Open CASCADE in uvožena v ProEngineer? Wildfire 3.0
Za risanje modelov CAD celotne mrežne konstrukcije ali konstrukcije, ki vsebuje več kot en poenostavljeni I-profil, uporabimo robni dopolnjevalec edge iterator, ki ga sistematično vključimo npr. v C++ for zanko. Tako uporabimo zanko za vsak izbrani izhodiščni rob kateregakoli prej določenega profila. V našem primeru velja zančje za poenostavljeni I-profil.

Literatura

1 OpenCascadeTM 3D modelling kernel. OpenCascade inc. 2009, ​http://www. opencascade.org/.
2 Copyright© 2003 by Open CASCADE – A. Immeuble, Domaine Technologique de Saclay 4, rue Rene Razel, 91400 SACLAY – France.
3 L. Kos, S. Kulovec, V. Zaletelj, J. Duhovnik, Support Structure for Freeform Arhitectural Desing (TMCE 2010).
4 Copyright© 2008 by Open CASCADE – Open CASCADE 6.3 Minor Release
5 J.-J. Risler, Mathematical Methods for CAD. Cambridge. etc., Cambridge University Press 1992.
6 Pierre Bézier, The mathematical basis of the UNISURF CAD system, Butterworths 1986.
7 Paul S. Heckbert, Graphics Gems IV, Academic Press 1994.

Pripravil:
asist. Simon Kulovec in asist.dr. Leon Kos