Manipuler les maillages non structurés¶
Les meshes non-structurées sont le type de maillage le plus utilisé. MEDCouplingUMesh est le nom de la classe en charge de représenter ces maillages dans MEDCoupling. MEDCouplingUMesh hérite de la classe MEDCouplingPointSet. MEDCouplingPointSet gère toutes les méthodes relatives au coordonnées. MEDCouplingUMesh a deux attributs en plus de ceux de MEDCouplingPointSet permettant de décrire la liste des noeuds contribuants à une cellule (i.e. la connectivité).
Objectifs¶
Le but ici est de manipuler des maillages non structurés (en extraire une partie, etc...). Plusieurs points seront traités dans cet exercice :
- modification des coordonnées d’un maillage
- extraction d’une coupe d’un maillage
- extraire une partie de maillage à partir d’identifiants de cellules
- manipuler les indices, etc ...
- manipulation de la connectivité descendante

Début de l’implémentation¶
Importer le module Python MEDCoupling.
import MEDCoupling as mc
Construire un maillage. Ce maillage mesh3D contient artificiellement 2 types de cellules (mc.NORM_HEXA8 et mc.NORM_POLYHED) pour appréhender le mélange de types geometriques. mesh3D est un maillage extrudé contenant 18 cellules composées de 3 niveaux selon Z, chaque niveau ayant 6 cellules. Faire un bon gros copier-coller des lignes suivantes pour construire la mesh (l’intérêt de l’exercise vient après) :
coords=[0.,0.,0., 1.,1.,0., 1.,1.25,0., 1.,0.,0., 1.,1.5,0., 2.,0.,0., 2.,1.,0., 1.,2.,0., 0.,2.,0., 3.,1.,0.,
3.,2.,0., 0.,1.,0., 1.,3.,0., 2.,2.,0., 2.,3.,0.,
0.,0.,1., 1.,1.,1., 1.,1.25,1., 1.,0.,1., 1.,1.5,1., 2.,0.,1., 2.,1.,1., 1.,2.,1., 0.,2.,1., 3.,1.,1.,
3.,2.,1., 0.,1.,1., 1.,3.,1., 2.,2.,1., 2.,3.,1.,
0.,0.,2., 1.,1.,2., 1.,1.25,2., 1.,0.,2., 1.,1.5,2., 2.,0.,2., 2.,1.,2., 1.,2.,2., 0.,2.,2., 3.,1.,2.,
3.,2.,2., 0.,1.,2., 1.,3.,2., 2.,2.,2., 2.,3.,2.,
0.,0.,3., 1.,1.,3., 1.,1.25,3., 1.,0.,3., 1.,1.5,3., 2.,0.,3., 2.,1.,3., 1.,2.,3., 0.,2.,3., 3.,1.,3.,
3.,2.,3., 0.,1.,3., 1.,3.,3., 2.,2.,3., 2.,3.,3.]
conn=[0,11,1,3,15,26,16,18, 1,2,4,7,13,6,-1,1,16,21,6,-1,6,21,28,13,-1,13,7,22,28,-1,7,4,19,22,-1,4,2,17,19,-1,2,1,16,17,-1,16,21,28,22,19,17,
1,6,5,3,16,21,20,18, 13,10,9,6,28,25,24,21, 11,8,7,4,2,1,-1,11,26,16,1,-1,1,16,17,2,-1,2,17,19,4,-1,4,19,22,7,-1,7,8,23,22,-1,8,11,26,23,-1,26,16,17,19,22,23,
7,12,14,13,22,27,29,28, 15,26,16,18,30,41,31,33, 16,17,19,22,28,21,-1,16,31,36,21,-1,21,36,43,28,-1,28,22,37,43,-1,22,19,34,37,-1,19,17,32,34,-1,17,16,31,32,-1,31,36,43,37,34,32,
16,21,20,18,31,36,35,33, 28,25,24,21,43,40,39,36, 26,23,22,19,17,16,-1,26,41,31,16,-1,16,31,32,17,-1,17,32,34,19,-1,19,34,37,22,-1,22,23,38,37,-1,23,26,41,38,-1,41,31,32,34,37,38,
22,27,29,28,37,42,44,43, 30,41,31,33,45,56,46,48, 31,32,34,37,43,36,-1,31,46,51,36,-1,36,51,58,43,-1,43,37,52,58,-1,37,34,49,52,-1,34,32,47,49,-1,32,31,46,47,-1,46,51,58,52,49,47,
31,36,35,33,46,51,50,48, 43,40,39,36,58,55,54,51, 41,38,37,34,32,31,-1,41,56,46,31,-1,31,46,47,32,-1,32,47,49,34,-1,34,49,52,37,-1,37,38,53,52,-1,38,41,56,53,-1,56,46,47,49,52,53,
37,42,44,43,52,57,59,58]
mesh3D = mc.MEDCouplingUMesh("mesh3D",3)
mesh3D.allocateCells(18)
mesh3D.insertNextCell(mc.NORM_HEXA8,conn[0:8]); mesh3D.insertNextCell(mc.NORM_POLYHED,conn[8:51]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[51:59]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[59:67]); mesh3D.insertNextCell(mc.NORM_POLYHED,conn[67:110]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[110:118]);
mesh3D.insertNextCell(mc.NORM_HEXA8,conn[118:126]); mesh3D.insertNextCell(mc.NORM_POLYHED,conn[126:169]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[169:177]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[177:185]); mesh3D.insertNextCell(mc.NORM_POLYHED,conn[185:228]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[228:236]);
mesh3D.insertNextCell(mc.NORM_HEXA8,conn[236:244]); mesh3D.insertNextCell(mc.NORM_POLYHED,conn[244:287]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[287:295]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[295:303]); mesh3D.insertNextCell(mc.NORM_POLYHED,conn[303:346]); mesh3D.insertNextCell(mc.NORM_HEXA8,conn[346:354]);
myCoords = mc.DataArrayDouble(coords,60,3)
myCoords.setInfoOnComponents(["X [m]","Y [m]","Z [m]"])
mesh3D.setCoords(myCoords)
mesh3D.orientCorrectlyPolyhedrons()
mesh3D.sortCellsInMEDFileFrmt()
mesh3D.checkConsistencyLight()
renum = mc.DataArrayInt(60); renum[:15]=range(15,30) ; renum[15:30]=range(15) ; renum[30:45]=range(45,60) ; renum[45:]=range(30,45)
mesh3D.renumberNodes(renum,60)
Convertir les unités¶
On convertit ici les coordonnées de mètres en centimètres. Cela paraît idiot mais c’est un très grand classique du couplage ...
mesh3D.getCoords()[:] *= 100.
mesh3D.getCoords().setInfoOnComponents(["X [cm]","Y [cm]","Z [cm]"])
Note
Il est important de mettre à jour les informations sur les composantes des coordonnées (les unités) pour éviter toute ambiguïté. INTERP_KERNEL library inclut un évaluateur d’unité.
Note
Noter l’astuce sur la première ligne [:] afin de récupérer la version inscriptible des coordonnées (et non une copie temporaire)
Trouver les différents niveaux¶
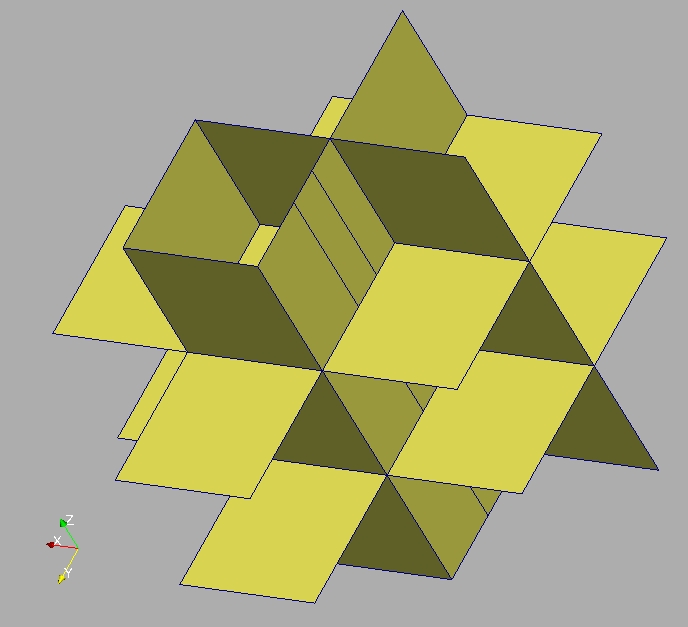
Le maillage est extrudé, il est donc très régulier, et aligné sur les axes Ox, Oy et Oz (cf figure). On veut connaître quelles sont les côtes Z des différentes couches de cubes. Extraire les différents niveaux en Z dans mesh3D, rangés de manière croissante. Utiliser la méthode DataArrayDouble.getDifferentValues() and DataArrayDouble.sort().
zLev = mesh3D.getCoords()[:,2]
zLev = zLev.getDifferentValues(1e-12)
zLev.sort() # In-place sort
Extraire des identifiants de cellules¶
Extraire les 6 identifiants des cellules de la seconde rangée suivant Oz. Il y a 3 possibilités pour faire cela. Nous allons les voir du plus simple au plus complexe.
- En utilisant buildSlice3D() :
Méthode très simple mais gourmande en CPU. Pour trouver la solution il suffit de définir un plan dont le vecteur normal est [0.,0.,1.] et passant par le point [0., 0., (zLev[1]+zLev[2])/2]. La méthode retourne deux choses : le maillage de coupe tmp (un maillage de mesh-dimension 2, mais de dimension spatiale 3) et pour chaque cellule 3D surfacique de tmp, l’identifiant de la cellule 3D (=un volume) coupée dans le maillage de départ
tmp, cellIdsSol1 = mesh3D.buildSlice3D([0.,0.,(zLev[1]+zLev[2])/2], [0.,0.,1.], 1e-12)
- En utilisant les barycentres des cellules de mesh3D :
L’utilisation des barycentres est une technique classique pour identifier un ensemble de cellules répondant à certains critères géométriques. Il s’agit d’abord de calculer les barycentres des cellules 3D de mesh3D (méthode MEDCouplingUMesh.computeCellCenterOfMass()). (Note: le nom – un peu trop long – de cette méthode hérite du passé. Le “AndOwner” indique le fait qu’en C++ l’appelant est responsable de la désallocation de l’objet retourné : il prend l’ownership du résultat).
Ensuite sélectionner la composante #2 des barycentres des cellules et mettre le résultat dans baryZ. Ensuite il suffit de selectionner dans baryZ les tuples qui sont dans l’intervalle [zLev[1], zLev[2]]. Les identifiants de ces tuples (i.e. leur index dans baryZ) est directement un identifiant de cellule car computeCellCenterOfMass() retourne un tableau indéxé par les numéros de cellule.:
bary = mesh3D.computeCellCenterOfMass() baryZ = bary[:,2] cellIdsSol2 = baryZ.findIdsInRange(zLev[1], zLev[2])
- En utilisant MEDCouplingMappedExtrudedMesh :
C’est la méthode exclusivement basée sur la connectivité nodale pour déduire l’extrusion. Les coordonnées sont ici ignorées. Pour construire un MEDCouplingMappedExtrudedMesh deux objets sont requis. Le maillage non-structuré 3D représentant en fait un maillage extrudé, et un maillage non structuré 3D surfacique (mesh-dim 2) reposant sur les mêmes coordonnéees, à partir duquel l’extrusion sera calculée. Commencer par construire le maillage 3D surfacique. Pour ce faire il suffit de repérer les noeuds appartenant à 1e-10 près de plan de vecteur normal [0.,0.,1.] et passant par [0.,0.,zLev[0]] (MEDCouplingUMesh.findNodesOnPlane()). Ensuite appeler MEDCouplingUMesh.buildFacePartOfMySelfNode() pour construire mesh2D (lire la doc de la fonction).
nodeIds = mesh3D.findNodesOnPlane([0., 0., zLev[0]], [0.,0.,1.], 1e-10) mesh2D = mesh3D.buildFacePartOfMySelfNode(nodeIds, True)
Il est alors possible de construire un maillage extrudé extMesh à partir de mesh3D et de mesh2D. Un maillage extrudé se construit en reconnaissant un maillage non structuré comme étant l’extrusion d’un maillage de dimension n-1 (avec n la dimension initiale de mesh3D, ici 3). Si cela n’est pas le cas, la construction plante. Le maillage 2D est forcément en haut ou en bas du 3D volumique, et le dernier entier spécifie la cellule à partir de laquelle le fil de fer 1D guidant l’extrusion sera construit :
extMesh = mc.MEDCouplingMappedExtrudedMesh(mesh3D, mesh2D, 0)
On a alors la garantie que, dans extMesh, les cellules sont ordonnées par niveau Z croissant. Il suffit de récupérer le 2ème niveau (MEDCouplingMappedExtrudedMesh.getMesh3DIds()).
n_cells = mesh2D.getNumberOfCells() cellIdsSol3 = extMesh.getMesh3DIds()[n_cells:2*n_cells]
On vérifie alors que les 3 solutions sont les mêmes :
print cellIdsSol1.getValues()
print cellIdsSol2.getValues()
print cellIdsSol3.getValues()
Extraire une sous partie d’un maillage 3D¶
Utiliser les identifiants de cellules cellIdsSol2 obtenus précédemment pour extraire une sous-partie de mesh3D, c’est-à-dire un maillage avec un sous-ensemble des cellules de mesh3D.
mesh3DPart = mesh3D[cellIdsSol2]
Note
En C++ la méthode sous-jacente invoquée (et par ailleurs aussi disponible en Python) s’appelle mesh3DPart = mesh3D.buildPartOfMySelf(cellIdsSol2,True)
Note
Le type géométrique ne rentre pas du tout en compte ici. L’instruction précédente prend les cellules dans l’ordre où elles sont disponibles dans le maillage initial.
L’objet mesh3DPart contient len(cellIdsSol2) cellules désormais. La cellule #0 de mesh3DPart correspond à la cellule avec l’identifiant cellIdsSol2[0] de mesh3D, et ainsi de suite. Ainsi cellIdsSol2 peut être vu comme un tableau new-2-old.
A ce point, mesh3DPart repose sur une copie du tableau de coordonnées de mesh3D, c’est-à-dire 60 nodes. Seuls 30 sont effectivement utilisés. Pour retirer les noeuds orphelins de mesh3DPart invoquer simplement MEDCouplingUMesh.zipCoords().
mesh3DPart.zipCoords()
Maintenant, mesh3DPart repose sur 30 nodes et possède 6 cellules. Pour être prêt aux I/O MED-fichier, il est alors important de voir si mesh3DPart est bien ordonné, c’est-à-dire si ses cellules sont bien rangées par type géométrique. On commence par inspecter l’état actuel :
print mesh3DPart.advancedRepr()
La fonction suivante fait le même travail :
print mesh3DPart.checkConsecutiveCellTypesAndOrder([mc.NORM_HEXA8, mc.NORM_POLYHED])
Ou bien :
print mesh3DPart.checkConsecutiveCellTypes()
On voit que mesh3DPart contient 6 cellules, quatre HEXA8 puis deux POLYHED. Les cellules sont bien groupées par type géométrique. Si ce n’était pas le cas, on aurait pu invoquer MEDCouplingUMesh.sortCellsInMEDFileFrmt().
Extraire des cellules alignées sur une ligne 3D¶
On souhaite extraire de mesh3D les 3 cellules dont les barycentres sont le long de la ligne portée par v = [0.,0.,1.] et passant par pt = [250.,150.,0.]. Il y a deux solutions.
les barycentres de mesh3D : même principe qu’au-dessus.
baryXY = bary[:,[0,1]] baryXY -= [250.,150.] magn = baryXY.magnitude() cellIds2Sol1 = magn.findIdsInRange(0.,1e-12)
utiliser le maillage extrudé extMesh : partant de l’unique cellule dans mesh2D dont le centre est en [250.,150.,0.], la méthdode MEDCouplingMappedExtrudedMesh.getMesh3DIds() retourne les identifiants de cellules rangée par rangée.
bary2 = mesh2D.computeCellCenterOfMass()[:,[0,1]] bary2 -= [250.,150.] magn = bary2.magnitude() ids = magn.findIdsInRange(0.,1e-12) idStart = int(ids) # ids is assumed to contain only one value, if not an exception is thrown ze_range = range(idStart,mesh3D.getNumberOfCells(),mesh2D.getNumberOfCells()) cellIds2Sol2 = extMesh.getMesh3DIds()[ze_range]
Maintenant on construit cette sous partie de mesh3D en utilisant cellIds2Sol1 ou cellIds2Sol2:
mesh3DSlice2 = mesh3D[cellIds2Sol1]
mesh3DSlice2.zipCoords()
Duplication, translation et aggrégation de maillages¶
Cette partie de l’exercice est intéressante pour construire des maillages complexes, ou pour aggréger des parties de maillages venant de différents processeurs.
On cherche ici à dupliquer mesh3DSlice2, le translater et l’aggréger avec l’original.
Effectuer une copie complète de mesh3DSlice2 (aussi appelée deep copy) sous le nom mesh3DSlice2bis. Sur cette copie effectuer une translation de v=[0.,1000.,0.]. Puis aggréger mesh3DSlice2 avec sa copie translatée mesh3DSlice2bis, en utilisant MEDCouplingUMesh.MergeUMeshes().
mesh3DSlice2bis = mesh3DSlice2.deepCopy()
mesh3DSlice2bis.translate([0.,1000.,0.])
mesh3DSlice2All = mc.MEDCouplingUMesh.MergeUMeshes([mesh3DSlice2,mesh3DSlice2bis])
mesh3DSlice2All.writeVTK("mesh3DSlice2All.vtu")
Note
Pour information pour merger deux (ou plus) maillages non structurés, il faut invoquer MEDCouplingUMesh.MergeUMeshes() puis MEDCouplingUMesh.mergeNodes() sur le résultat, et enfin MEDCouplingUMesh.zipConnectivity().
Connectivité descendante¶
Le but ici est de présenter la notion de connectivité descendante (descending connectivity).
La connectivité descendante représente les éléments de dimension n-1 constituant chacune des cellules de dimension n (avec donc n la dimension du maillage, mesh-dim). Par exemple, pour un maillage de dimension 3 (les cellules sont des volumes 3D), cela donne l’ensemble des faces (des surfaces 2D) bordant ces volumes.
A titre d’exemple, on se propose dans notre cas de récupérer les faces internes du maillage mesh3D. Pour cela il est nécessaire de construire le maillage descendant de mesh3D (stocké dans mesh3DSurf) c’est-à-dire le maillage de mesh-dimension 2 (soit mesh3D.getMeshDimension()-1) constitué des faces bordant chacune des cellules (ici des volumes 3D) de mesh3D. La méthode MEDCoupling.buildDescendingConnectivity() calcule ce maillage, et retourne en même temps des tableaux de correspondance. Ces tableaux font le lien entre les identifiants des cellules de mesh3D vers les identifiants de cellules de mesh3DSurf, et vice-et-versa.
Une face de mesh3DSurf est dite interne, si et seulement si, elle est partagée par plus d’une cellule 3D de mesh3D. Les 3ème et 4ème paramètres de sortie de la fonction donnent le lien entre une face et ses cellules parentes (i.e. le ou les volumes qu’elle délimite). Ce lien est exprimé au format indirect index vu dans le premier exercice Manipuler le format “indirect index”.
mesh3DSurf, desc, descIndx, revDesc, revDescIndx = mesh3D.buildDescendingConnectivity()
numberOf3DCellSharing = revDescIndx.deltaShiftIndex()
cellIds = numberOf3DCellSharing.findIdsNotEqual(1)
mesh3DSurfInside = mesh3DSurf[cellIds]
mesh3DSurfInside.writeVTK("mesh3DSurfInside.vtu")
Ce genre de manipulation est très utile pour accéder au voisinage d’une ou plusieurs cellules d’un maillage non-structuré.